2400 · 皆さんは 「連立方程式」 と聞けば、「 と 」、「式が2つある」といったイメージを持つのかもしれません。 しかし、実は連立方程式は必ずしも式が2つではないのです! 3つのときもあれば、場合によっては4つのこともそれは、x=2 のとき y=5 という解です。 これを簡単に求める方法が「連立方程式」なのです。 今度は、グラフに目を向けます。 y=2x1 のグラフですが、 このグラフ、実は 二元一次方程式 y=2x1 の解の集まりなのです。無数にある解1つ1つが座標上の点であり、その無数の点が集まって 線を構成しています。 そろそろ予想できてきた かもしれませんが、グラフ上の2本のまずトムの持ち分をx、ジムをyとすれば、x+y=21、x-y=という連立方程式になります。 これを解くと X=5、Y=05となり、これ以外のXとYの解は導き出されない ことがわかります。
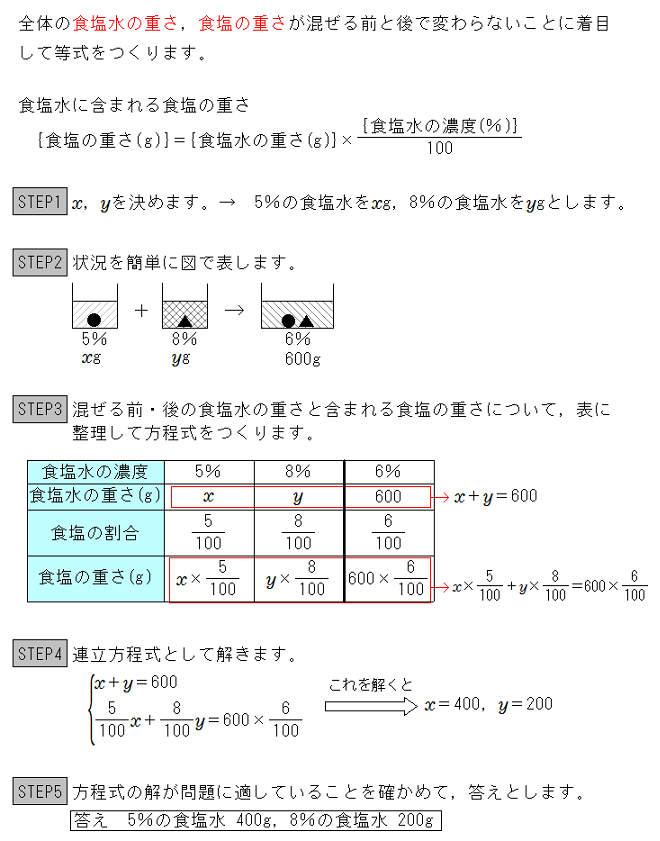
連立方程式 食塩水の問題で連立方程式をつくるコツ 中学数学 定期テスト対策サイト
連立 方程式 わからない
連立 方程式 わからない-第2章 連立方程式 <前: L14 いろいろな連立方程式 の問題 L15 連立方程式-個数・代金編 の解答 :次> 練習問題1 ある文具店でペンとノートを買おうとしたところ、ペン3本とノート2冊だと合計代金は660円、ペン5本とノート4冊だと合計代金は10円連立方程式の問題 Try IT(トライイット)の連立方程式の様々な問題を解説した映像授業一覧ページです。 連立方程式を探している人や問題の解き方がわからない人は、単元を選んで問題と解説の映像授業をご覧ください。




例題 演習問題付き 連立方程式の解き方と失敗しないコツをわかりやすく解説します 中学受験ナビ
0721 · 連立方程式では 求める値が2つ あるので、計算の手順や方法が増えていくのが厄介なんです。 連立方程式は、定期テストはもちろん、高校入試でも必ず出題されるので、絶対に取りこぼしのないようにしていきましょう!連立方程式 解と係数 連立文章題(整数問題1) 連立文章題(整数問題2) 連立文章題(個数と代金1) 連立文章題(個数と代金2) 連立文章題2(濃度) 連立文章題(割合) 連立文章題(速さ) 連立文章題(いろいろ) · 回答数: 2 件 中学の連立方程式の問題でわからない問題があるのでどうやって解くのか教えてくださいm (_ _)m 4x2y=24 3x-3y=9 通報する この質問への回答は締め切られました。 質問の本文を隠す A 同じカテゴリの新着質問 A 回答 (2件)
連立方程式とは {7x2y =5 2x5y = 8 のように2つ以上の方程式を組み合わせたものが 連立方程式 である。 組み合わせた, どの方程式も成り立たせるような文字の値の組が連立方程式の解となる。 中学で扱うのは上記のような2元1次方程式の連立方程式である。連立方程式とは、2つ以上の方程式を組み合わせたもののことを言います。 特に、今回からの数学で習う連立方程式では、 2元1次方程式 について扱っていくことになります。 (新しい単語を次々と出してしまってごめんなさい。 ) 2元1次方程式とは何かといいますと、式中に 次数が1 の文字が 2種類 ある方程式の事を言います。 言葉で説明しても分かりづらいとS わからない数量をxとyで置いて2つの方程式をつくる。 S 連立方程式をつくれば、後はそれを解けばよい。 S 解くときには、文字の係数をそろえ
· 中学校 夏の宿題に焦ってます 答えを写すのは好きでは無いのですが 少しでもわからないとやる気が無くなってしまうタイプなので 連立方程式のとこで30分止まってます・・・ a:x+2y=3800 · すると、個数の関係と金額の関係から次の連立方程式が立式できる。 \(\begin{eqnarray} \left\{ \begin{array}{l} x y = 5 \\ 50x 100y = 400 \end{array} \right \end{eqnarray}\) なるほど。では、2つの式から\(x\)と\(y\)を何とかして求めましょう! · 文字式の連立方程式 こんにちわ。 わからない、問題があって、だれか親切に教えてくれるとうれしいです sinx+siny=0 cosX+cosy=1 の連立方程式を解く問題です。 0≦x




中学数学の解説21ページ目 三重の個人契約家庭教師




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット
· では、1つの等式の中にわからない文字が2つあったら・・ そう!等式も2つあればその答えを導き出せるのです! 例で言うとこんな感じかな・・ x y = 10 x – y = 2 これが連立方程式!両辺に1000をかけると、4000x+3000y=となります。 そして、上の式4000x+3000y=から、下の式3500x+3000y=を引きます。 すると、500x=4000。 つまり、x=8 (室)となります。 さあ、3人タイプの部屋 (y)は、何室かな? ――連立方程式を使えば、この問題も解決することができましたね。 でも、連立方程式って、私たちの生活でどう役に · Pocket 今回は、中2で学習する『連立方程式』の単元から食塩水の濃度に関する文章問題の解き方について解説していくよ! 濃度って聞くと なんかイヤ! っていう人も多いのではないでしょうか (^^;
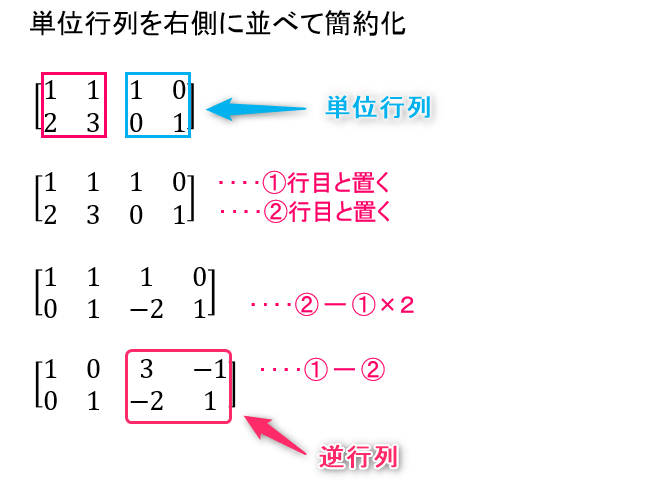



逆行列を求めて 実際に連立方程式を解いてみよう 線形代数を宇宙一わかりやすく解説してみるサイト



中学の数学 分数の連立方程式の解き方について質問です の両辺に15 Yahoo 知恵袋
二元連立方程式 110 /43件 表示件数 5 10 30 50 100 0 1 2342 男 / 歳未満 / 高校・専門・大学生・大学院生 / / 使用目的 時間短縮 ご意見・ご感想 関数電卓が手元にないとき、面倒事を押し付けれて非常に助かります。0807 · 連立方程式は2つの方程式の組み合わせで解答を出すので、そもそも方程式でミスを多く出している生徒はさらにミスが増えます。 確率でいえば、単独の方程式で正答率が5割だとすると、二つの場合だとかけ算になるので05×05=025 となり、4問に1問しか正解できないことになってしま1405 · 連立方程式とは、 進行方向がわかっている 2つのものが出会う場所を知りたいときに使用します。 先ほどの問題では、2人とも真っ直ぐに進むことがわかっていました。 進行方向を図で表すと、直線になりますよね。 一番初めに習う連立方程式は、直線を考えたと思います。 それが一番簡単だからです。 ここで重要なのは、「進行方向がわかっている」と




連立方程式 1 代入法と加減法 バカでもわかる 中学数学




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu
中2で学習する「連立方程式」は、 加減法、代入法のどちらでも 同じ答えになります 。 こう説明すると、 "ではなぜ、2つの解き方を習うの?" という疑問が出てきますよね。 この疑問の答えは、 ★ 代入法を使うと、速く解ける問題もあるから なのですが、連立方程式とは2つの文字(xとy)を含み、2つの式からなる方程式のこと。 連立方程式の解き方には 代入法 と 加減法 がある。 どちらの場合もxかyのどちらか 1つの文字を消去して解く 。 代入法 ≫ 加減法 片方の式が x = の形になっていれば、それを他方のxに代入することでxが消えてyだけの方程式ができる。 (y= の形ならyに代入する。 · ①行列の計算方法はわかるが、そもそもどんなときに行列を使うのかわからない! ②行列が使えるとどんなことが嬉しんだよ! 今回は、日常のあるあるから、行列が役立つ例を紹介します。 本記事の流れ: ①日常のあるあるから連立方程式を作る ②連立方程式を行列計算に置き換える
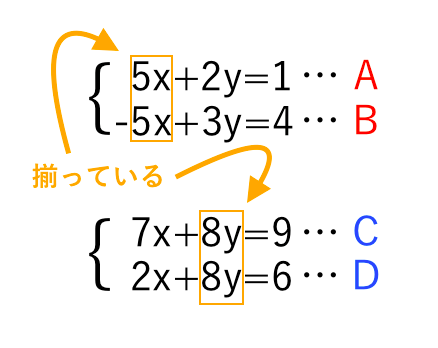



連立方程式の解き方 加減法 苦手な数学を簡単に
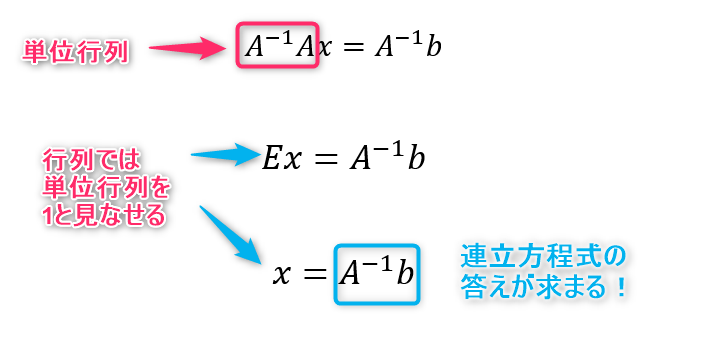



逆行列を求めて 実際に連立方程式を解いてみよう 線形代数を宇宙一わかりやすく解説してみるサイト
1600 · もう、ほんとに連立方程式が分からない笑 なんで、 1 回答 ベストアンサー 小学5年生 8ヶ月前 連立方程式の解き方です。 1 チャキ🦕⋆͛ 8ヶ月前 ありがとうございます!何パターンも作って頂き💦 凄くわかりやすいです! 1 この回答にコメントする 回答 T Yoshisaur Munchakoopasunofficial 8 · 連立方程式の解き方をみわける2つのコツ 連立方程式の解き方(加減法or代入法)を見分けるコツは、 代入法で解く特殊なケースを覚える ってことさ。 これを覚えちゃえば、 特殊なケースに出くわしたら「代入法」、 ソレ以外は「加減法」で解けるよね!たしかに見た目は連立方程式ですが、 別に連立方程式の問題ではありません。 ただの連立方程式の問題なら 中学生がやるべき問題です。 だから、この問題の出題者はこう言っているのです。 この問題は連立方程式の問題では決してなく 2次方程式の問題だぞ。惑わされるなよ




中学数学 連立方程式 文章題の解き方 立式のコツ




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
· 連立方程式の計算は ちょっとしたコツで 計算ミスを減らすことができます。 今回は 連立方程式で計算ミスをしないための コツについてお話していきます。 目次 hide 1 計算ミスを引き起こす原因は? 2 ミスを防ぐポイントは足し算!2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 (1) 答え 連立方程式の解き方 練習問題 (2) 答え 連立方程式の解き方 練習問題 (3) 答え 連立方程式の連立方程式がわからない人へ 中2数学「連立方程式」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「連立方程式の解き方」に関する6のポイントを覚える 「連立方程式の利用」に関する3のポイントを覚える まずはこれらのポイントをしっかり覚えてから、例題や練習にある問題を解いて「連立方程式」のわからないを克服しよう。
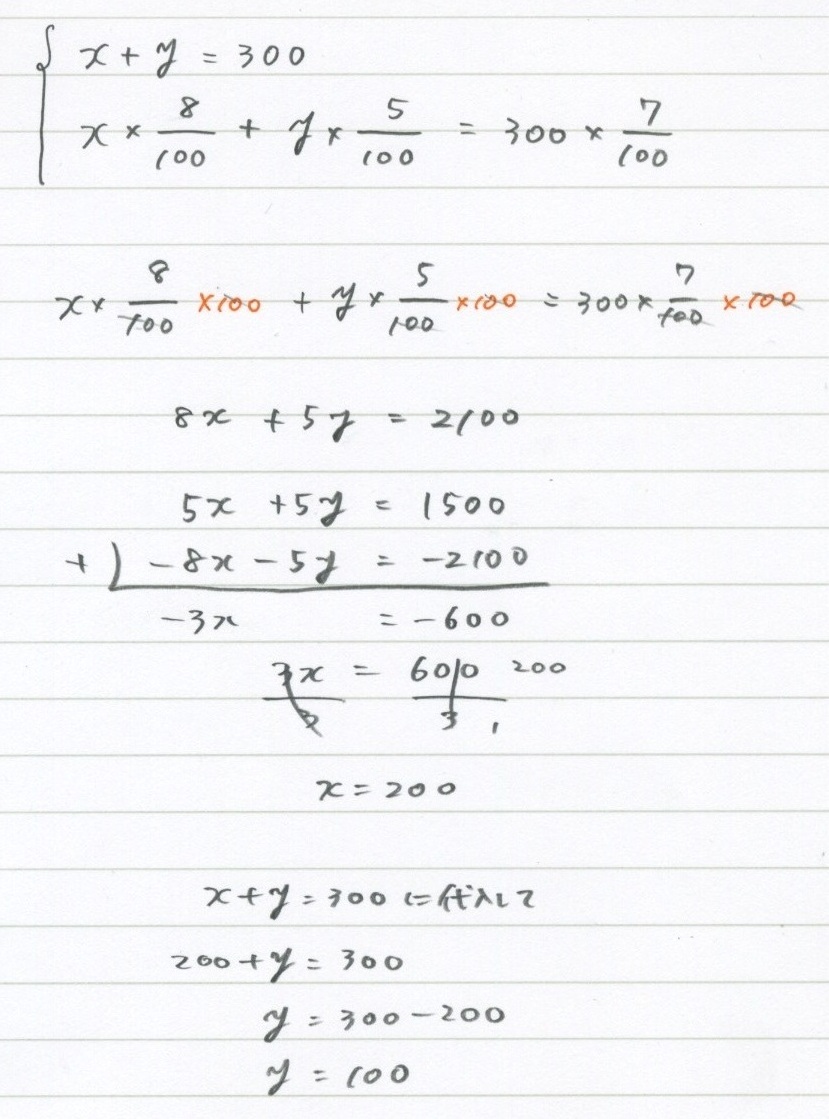



5 3 連立方程式 食塩水 勉強できようサイト




Hiro Academia 偏差値30からの早稲田慶應専門個別指導塾といえば
2619 · ・式が2つあるような連立方程式と形が異なりどうすればよいのか迷ってしまう ・解が与えられている場合、どう解けばよいのかわからない という人はぜひこの記事を読んでみて下さい。 · 2.わかっている数量、わからない数量をはっきりさせ、文字を使って連立方程式をつくる。 3.連立方程式を解く。 4.連立方程式の解が問題に適しているかどうかを確かめ、適していれば問題の答えとする。」 (2)
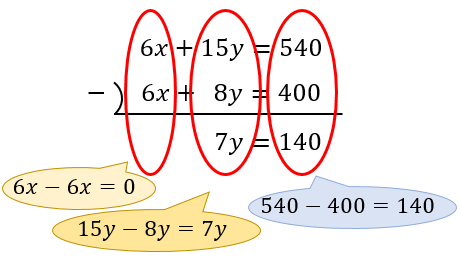



連立方程式 加減法 の解き方 なぜ加減法が成り立つか アタリマエ




100 Epic Best中2 数学 連立方程式の利用 問題 最高のぬりえ
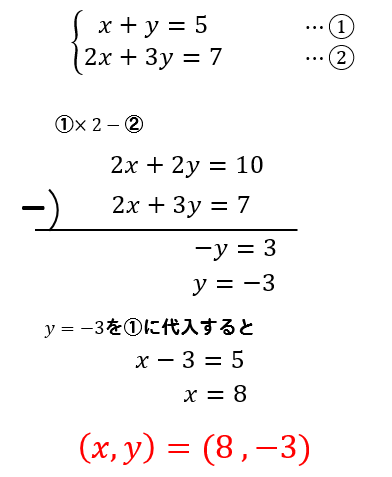



方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト
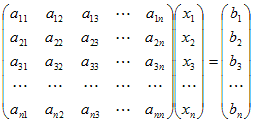



連立方程式の解き方




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




中学2年数学 連立方程式 加減法を使った連立方程式の解き方 実際に問題を解きながら解説 数学の面白いこと 役に立つことをまとめたサイト




文字が4つの連立方程式 Youtube




分数と小数の連立方程式の解き方が分かりません 教えてください Clear




Kistenkasten723 中2数学で連立方程式の解法として 最初に加減法 次に代入法を習う 画像は代入法を説明した直後の練習問題である 掛算 超算数 算数 算数教育 テスト 試験 文脈 さくらんぼ計算




例題 演習問題付き 連立方程式の解き方と失敗しないコツをわかりやすく解説します 中学受験ナビ




中2数学 連立方程式の文章題 割合 例題編 映像授業のtry It トライイット
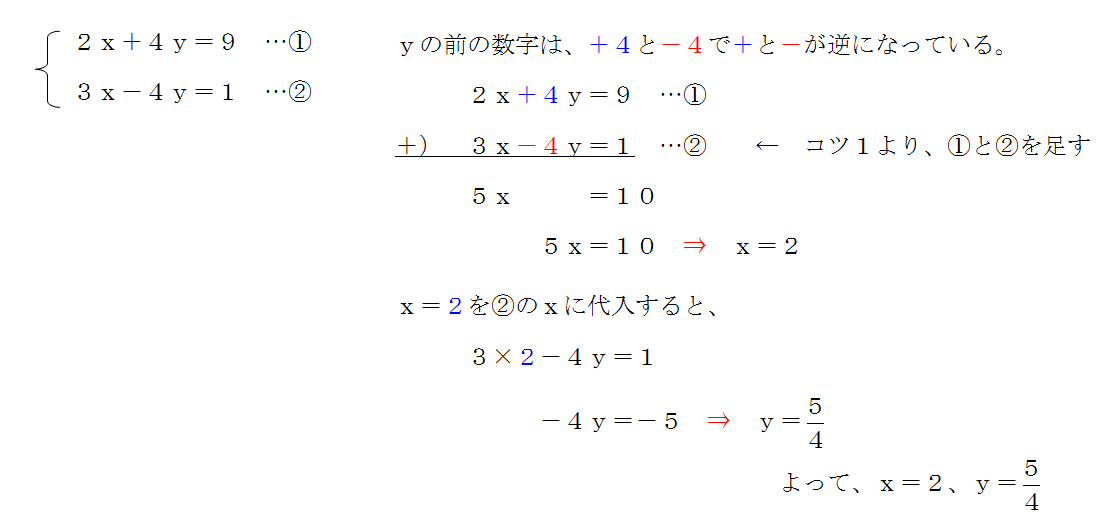



連立方程式の解き方 問題の文字を消すことが解き方のコツだ 三重の個人契約家庭教師




ロイヤリティフリー分数 の 連立 方程式 解き方 最高のぬりえ




数学 中2 17 連立方程式 代入法編 Youtube




三元連立方程式 2 中2数学 Youtube




100 Epic Best中2 数学 連立方程式の利用 問題 最高のぬりえ



Search Q E9 80 A3 E7 Ab 8b E4 B8 8d E7 Ad E5 8f Tbm Isch




連立方程式の解き方 の問題のわからないを5分で解決 映像授業のtry It トライイット




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト




解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




連立方程式の解き方を理解しよう さわやか さくらぐみ




例題 演習問題付き 連立方程式の解き方と失敗しないコツをわかりやすく解説します 中学受験ナビ




高校数学で学習する連立方程式の解き方まとめ 数スタ




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




連立方程式 食塩水の問題で連立方程式をつくるコツ 中学数学 定期テスト対策サイト




この連立方程式の問題でテストに出るんですけど解き方がよく分からないので解説して下さい Clear
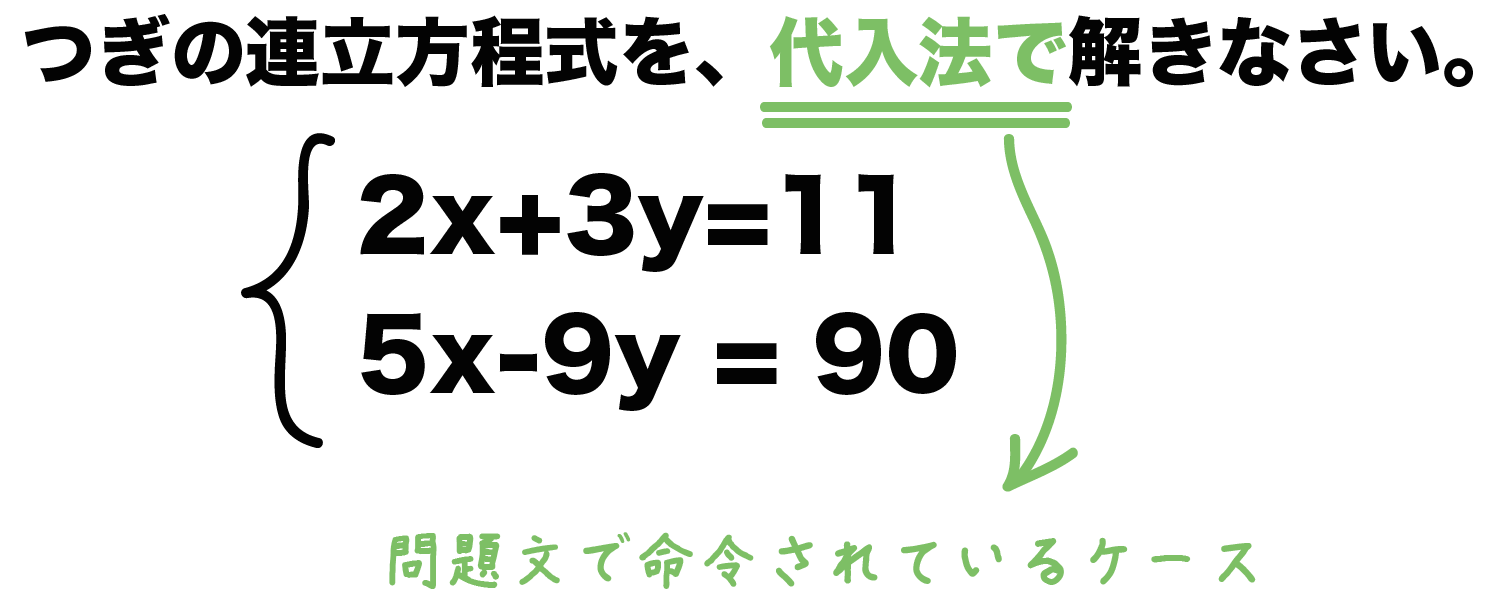



超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく




加減法 連立方程式の解き方 中学数学 By じょばんに マナペディア




分母のところに文字がある 連立方程式の計算がちょっとよくわからないです Clear




中学2年数学 連立方程式 加減法を使った連立方程式の解き方 実際に問題を解きながら解説 数学の面白いこと 役に立つことをまとめたサイト
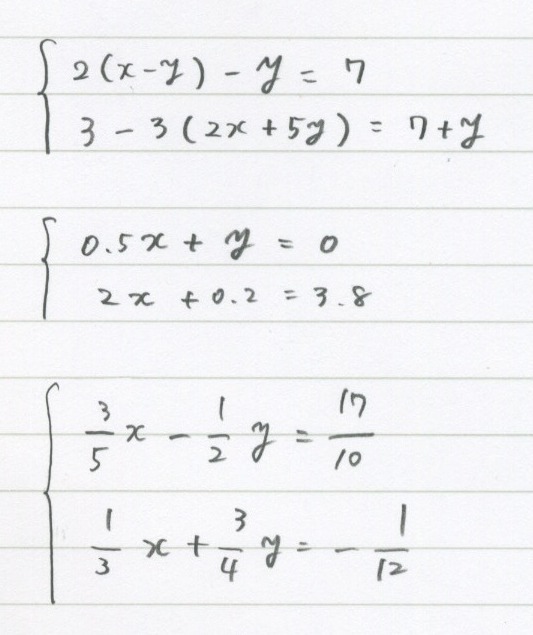



ロイヤリティフリー分数 の 連立 方程式 解き方 最高のぬりえ




高校数学で学習する連立方程式の解き方まとめ 数スタ



至急お願いします この連立方程式が解をもつように定数kを定 Yahoo 知恵袋
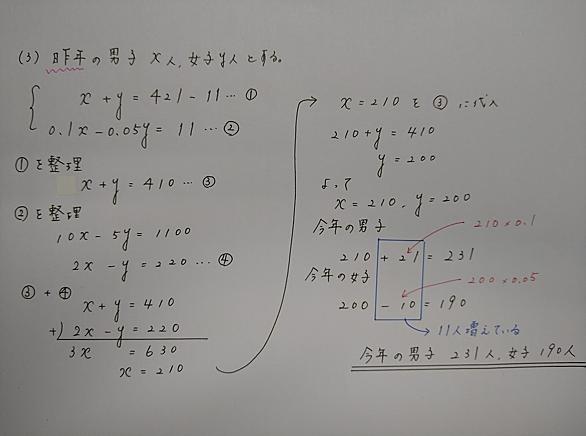



連立方程式とは サイエンスの人気 最新記事を集めました はてな
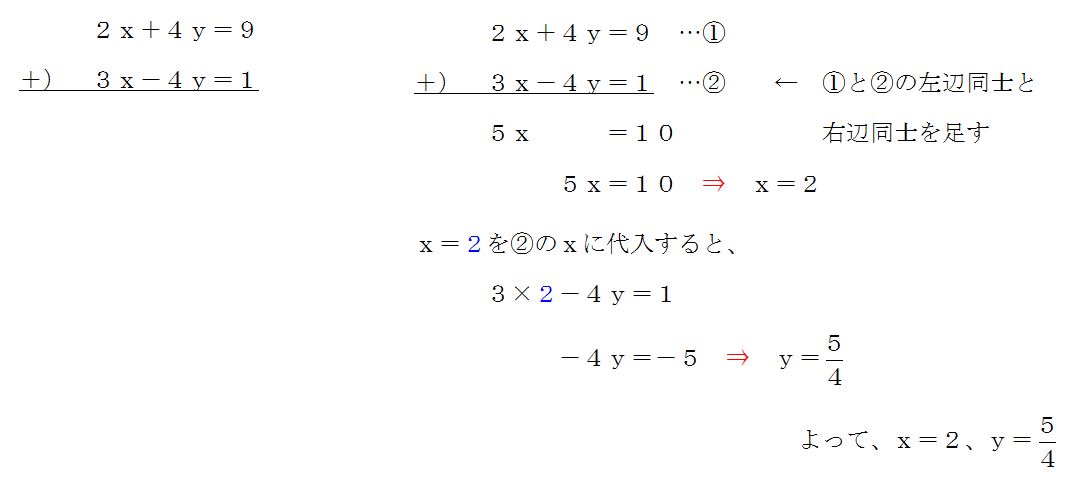



連立方程式の解き方 問題の文字を消すことが解き方のコツだ 三重の個人契約家庭教師




例題 演習問題付き 連立方程式の解き方と失敗しないコツをわかりやすく解説します 中学受験ナビ




連立3元1次方程式 まなびの学園




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
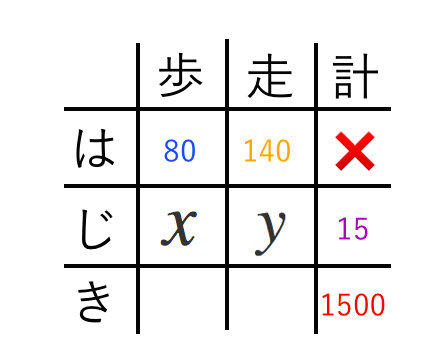



連立方程式の利用 速さ 練習問題 苦手な数学を簡単に




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点




連立方程式の解き方 問題の文字を消すことが解き方のコツだ 三重の個人契約家庭教師




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス
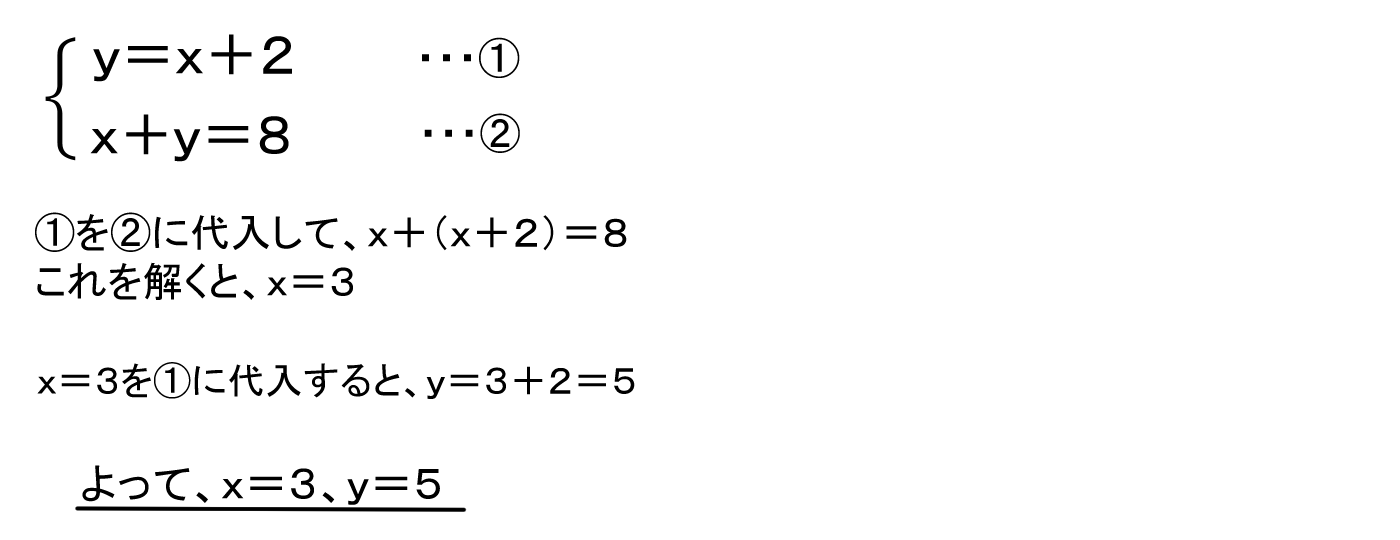



連立方程式 1 代入法と加減法 バカでもわかる 中学数学




超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく
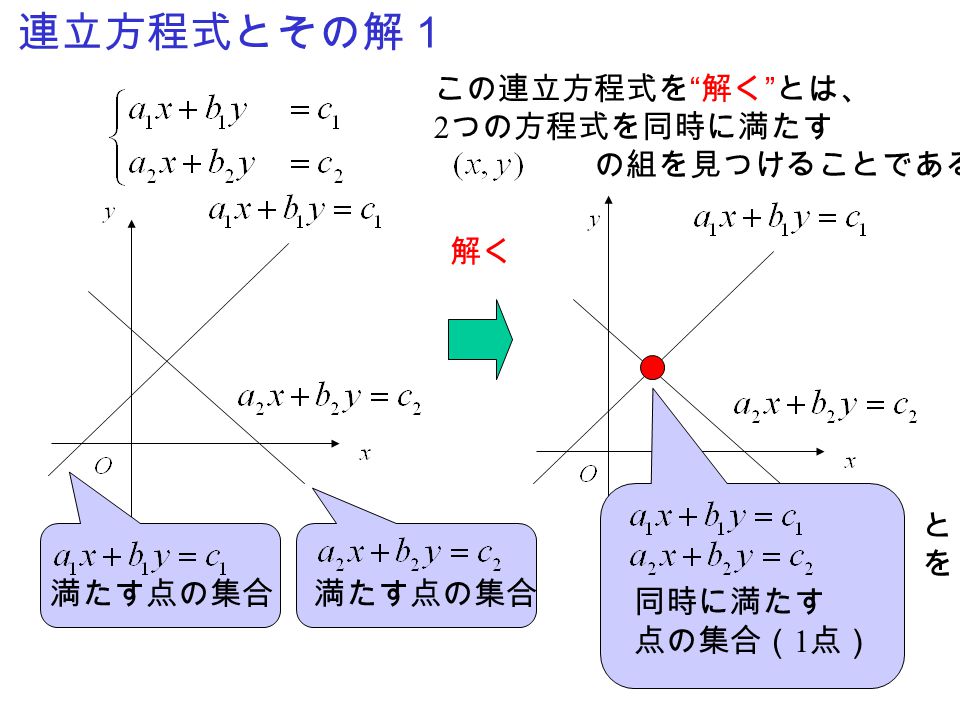



5 連立一次方程式 Ppt Video Online Download




中2数学 a b cの連立方程式 例題編 映像授業のtry It トライイット




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




連立方程式の解き方 3 きっずゼミ子育て応援ブログ




連立方程式の利用 文章題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




分数と小数の連立方程式の解き方が分かりません 教えてください Clear




文字について解く方法 xについて解くなら等式の左辺にもってこよう 中学や高校の数学の計算問題




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト



1




数学 中2 15 連立方程式 加減法の基本編 Youtube




連立方程式 A B C の形をした方程式の解き方をイチから解説 Youtube




数学 中2 14 連立方程式 準備編 Youtube




5 3 連立方程式 食塩水 勉強できようサイト




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
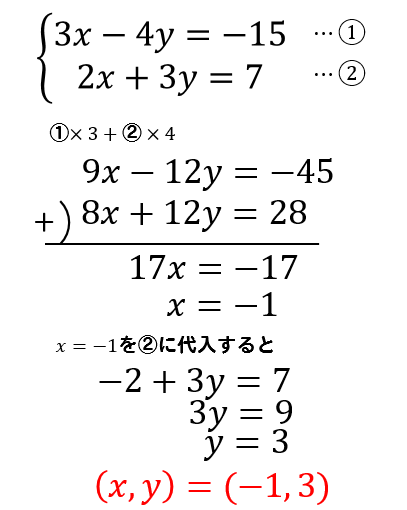



連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ



1
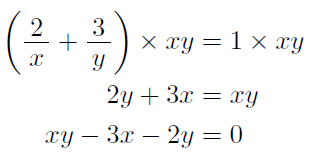



置き換えによる連立方程式 まなびの学園




連立方程式とは 中2数学 Enjoy Study 神松寺校 福岡市城南区神松寺の個別指導学習塾




連立方程式の解き方 移項と展開 Youtube



1
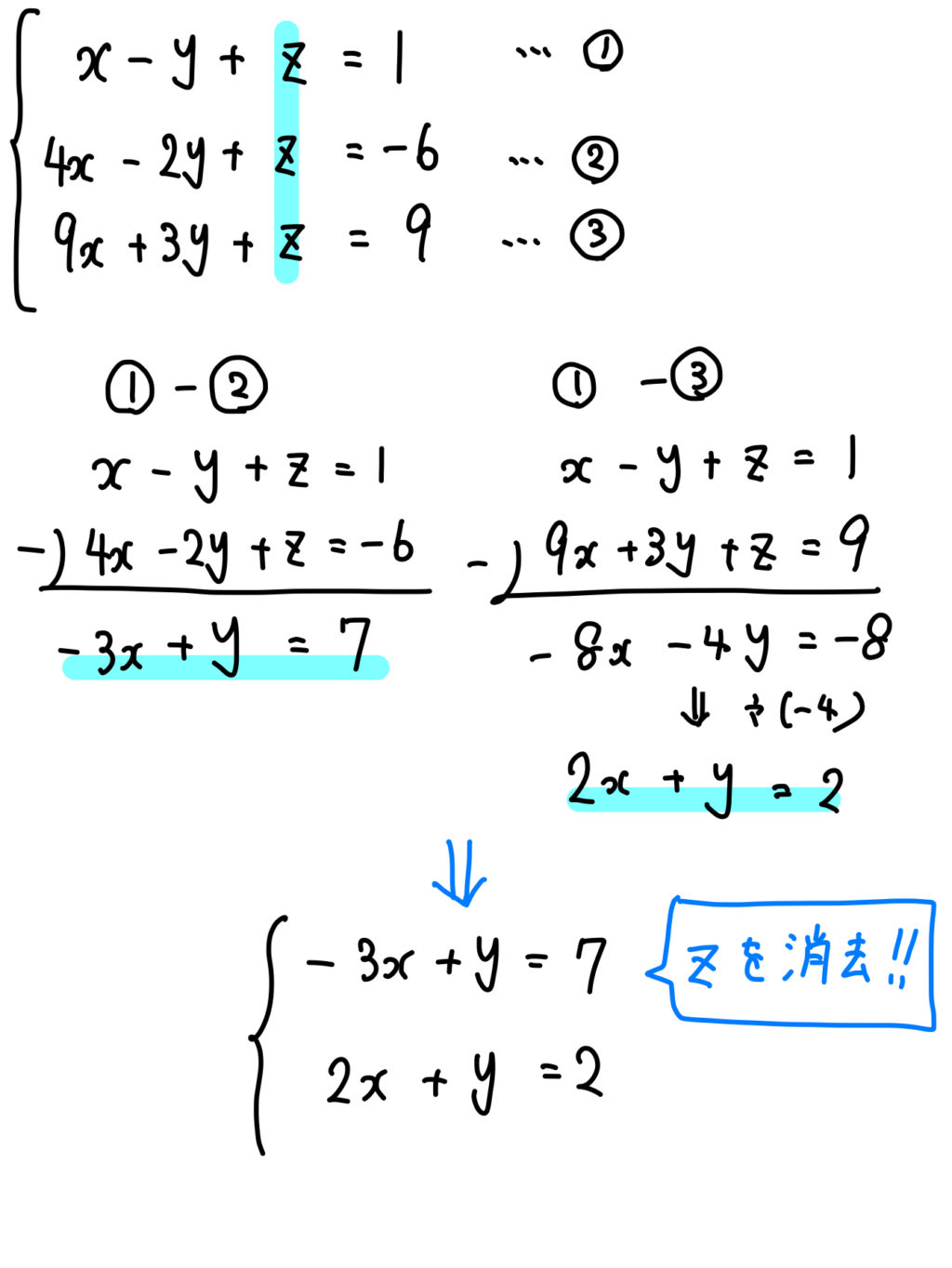



高校数学で学習する連立方程式の解き方まとめ 数スタ
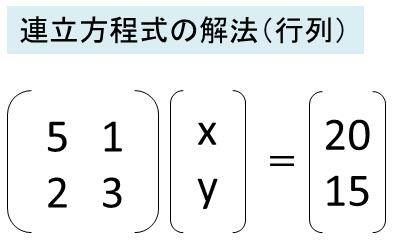



Excel エクセルで連立一程式を解く方法 計算問題を解いてみよう 連立一次方程式




こんな風に なぜ連立方程式で交点がわかるんですか Clear




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




連立方程式 1 代入法と加減法 バカでもわかる 中学数学



千葉工業大学の学生です 連立方程式がわからないのですが どんな勉強をすれば Yahoo 知恵袋
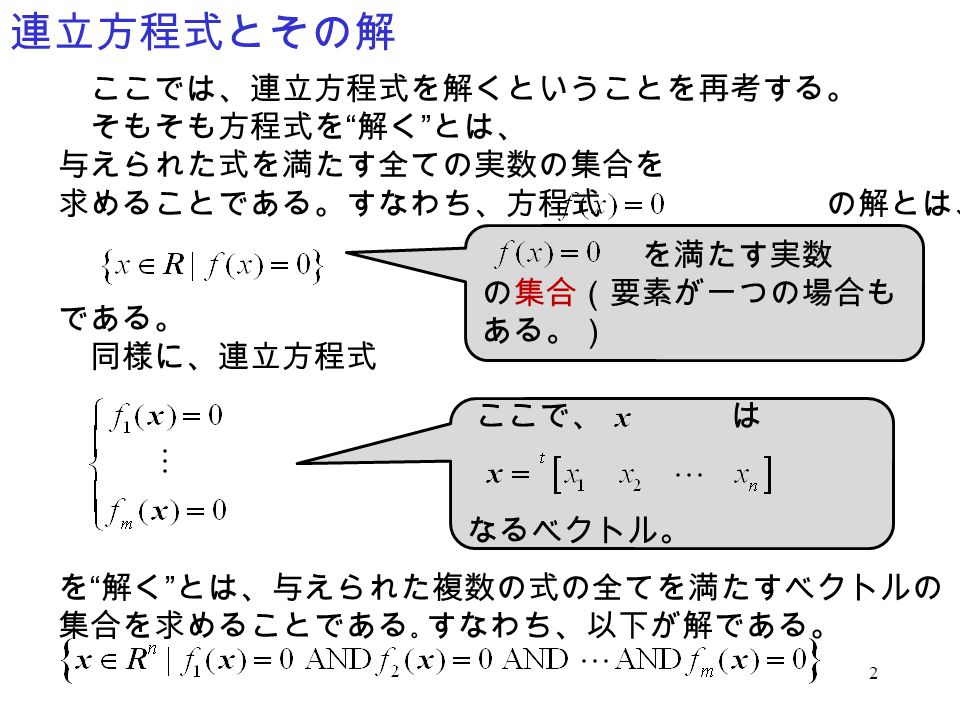



5 連立一次方程式 Ppt Video Online Download




5 1 連立方程式 基本 勉強できようサイト
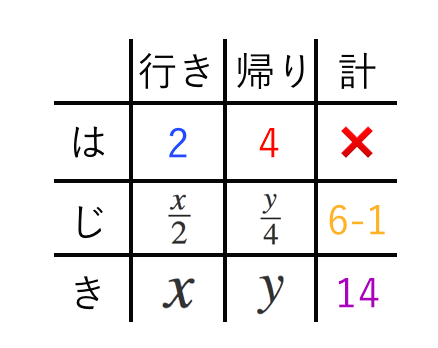



連立方程式の利用 速さ 練習問題 苦手な数学を簡単に




連立方程式を小学生に教える



連立方程式において結果0 0になるときなぜ共通な解は全ての解の組 Yahoo 知恵袋



数学の話なんですが 連立方程式の加減法が少しわからないので教えて Yahoo 知恵袋




連立方程式の利用 文章題の基本問題 合計 教遊者



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス




これを A Bについての連立方程式として解くと これってどうやるんですか Clear




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu




中学数学2年 連立方程式の利用 整数 受験の月




連立方程式の解き方 Youtube




一次方程式の解の求め方 数学fun




中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校数学で学習する連立方程式の解き方まとめ 数スタ



0 件のコメント:
コメントを投稿